Anonym
02.12.2021 um 22:43 Uhr
Zwei Flächenstücke: Uneigentliche Integrale
Die Graphen von f(x)= 2x+2 und g(x)= 4/x^3 begrenzen gemeinsam mit der x-Achse eine bis ins Unendliche reichende Fläche A. Fertigen Sie eine Skizze an und berechnen Sie den Inhalt A.
Hallo, weiß jemand vielleicht wie ich hier vorgehen muss, also bei der Rechnung?
Die Graphen von f(x)= 2x+2 und g(x)= 4/x^3 begrenzen gemeinsam mit der x-Achse eine bis ins Unendliche reichende Fläche A. Fertigen Sie eine Skizze an und berechnen Sie den Inhalt A.
Hallo, weiß jemand vielleicht wie ich hier vorgehen muss, also bei der Rechnung?
Anhand der Skizze erkennt man, dass man die Gesamtfläche in 2 Teilflächen aufteilen kann:
Die Fläche A1 unter dem Graphen von f(x) von x=-1 bis x=1. Dieses Integral ergibt 4.
Die Fläche A2 unter dem Graphen von g(x) von x=1 bis x = "unendlich".
Um ein solches "uneigentliches Integral" mit einer Grenze im Unendlichen zu berechnen, berechnet man zunächst das Integral von x=1 bis zur einem allgemeinen Wert x=a. Danach lässt man das a unendlich groß werden und schaut, welchen Grenzwert das Integral dann annimmt:
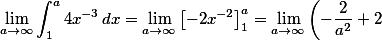)
Dieser Term geht für große a gegen 2, da der Bruch gegen Null geht.
Also hat die Fläche A2 als Grenzwert den Flächeninhalt 2.
Die Fläche A1 unter dem Graphen von f(x) von x=-1 bis x=1. Dieses Integral ergibt 4.
Die Fläche A2 unter dem Graphen von g(x) von x=1 bis x = "unendlich".
Um ein solches "uneigentliches Integral" mit einer Grenze im Unendlichen zu berechnen, berechnet man zunächst das Integral von x=1 bis zur einem allgemeinen Wert x=a. Danach lässt man das a unendlich groß werden und schaut, welchen Grenzwert das Integral dann annimmt:
Dieser Term geht für große a gegen 2, da der Bruch gegen Null geht.
Also hat die Fläche A2 als Grenzwert den Flächeninhalt 2.






